Let’s look at the operation of DNSSEC and its use of public key cryptographic algorithms.
The DNSSEC specification does not define in advance which algorithm you should use to generate the digital signature records for a DNSSEC-signed zone. And that’s a very good thing. The issue here is that cryptographic algorithms do not generate computationally impossible problems. Instead, they generate computationally infeasible problems. It’s not that you couldn’t crack some cyphertext if you tried hard enough and tried for long enough. It’s just that the search space is intentionally set to be sufficiently large that no matter how hard you try it will still probably take a geological eon or two, or perhaps even a period measured at the same scale as the age of the cosmos itself!
However, this concept of what is infeasible in practice is a moving target. Computers have, so far, continued to increase in capability at an exponential rate. If you consider these astonishing advances in computational capacity, then it’s clear that the threshold of what defines a computationally infeasible problem has changed dramatically. That means that if we want to preserve the privacy of encrypted information, then we’d like to pick a crypto algorithm and key profile that creates problems that are not only infeasible to solve on today’s computers but are infeasible on tomorrow’s computers as well. How far ahead you want to keep a secret determines how much additional computing capability you need to factor in with what you might think will still be an infeasible computational challenge some 5, 10 or even 50 years from now.
A very common cryptographic algorithm is RSA (named after the surnames of the original authors of the 1978 paper that described the algorithm, Ron Rivest, Adi Shamir and Leonard Adelman). RSA is a cryptographic algorithm that does both encryption and decryption using a variable key length. A shorter key is more efficient in terms of encryption and decryption but is not as robust. Longer keys are more expensive to use but offer greater robustness against efforts to break encoded data.
RSA is based on prime number operations using modular exponentiation. A basic principle behind RSA is the observation that it is practical to find three very large positive integers e, d, and n, such that with modular exponentiation for all integers m (with 0 ≤ m < n): (me)d ≡ m mod n. Even if you know the values of e and n, and even m, it can be extremely difficult to find the value of d.
The underlying premise here is that prime number factorisation of a very large composite integer can be hard, and if the number is the product of two very large prime numbers, then that task can be exceptionally hard. We’ve not devised (as yet) any better approach other than brute force enumeration. For example, the workload to factor a composite number that is the product of two prime numbers that are 512 bits long in binary notation was estimated in 1995 to take around 30,000 years using a 1 MIP (millions of instructions per second) computer. At that time, this scale of an infeasible challenge was a good match for that computing environment. (This threshold of feasibility was still considered reasonable some 8 years later, as I have a security practices publication from 2002 that observed that RSA using 512-bit keys was a practical profile for all but the most extreme security applications of 2002.)
To help understand the relative strength of cryptographic algorithms and keys there is the concept of a security level which the log base 2 of the number of operations to solve a cryptographic challenge. In other words, a security level of n implies that it will take 2n operations to solve the cryptographic challenge. Table 1 shows the security level for various RSA key lengths.
| Security Level (bits) | RSA Key Length (bits) |
| 80 | 1,024 |
| 112 | 2,048 |
| 128 | 3,072 |
| 140 | 4,096 |
| 192 | 7,680 |
Table 1 – Security level of various RSA key sizes
Things change in this space, and these days estimates of a minimal acceptable security strength that will provide protection across the coming decade points to the use of SHA-256 in conjunction with RSA with 2,048-bit keys, or a security level of 112 bits. However, if we want to encrypt data today with a protected secure lifetime of greater than 10 years then it looks like we may be looking at SHA-384 and RSA with 4,096-bit keys, or in other words a security level of more than 128 bits. Of course, these estimates don’t factor in the impact of any future use of quantum computing.
Developments in Quantum Computers and Cryptography
Taking this into account dramatically increases the resources required to factor 2048-bit numbers. In 2015, researchers estimated that a quantum computer would need a billion qubits to do the job reliably. That’s significantly more than the 70 qubits in today’s state-of-the-art quantum computers.
On that basis, security experts might well have been able to justify the idea that it would be decades before messages with 2048-bit RSA encryption could be broken by a quantum computer.
>Now Gidney and Ekerå have shown how a quantum computer could do the calculation with just 20 million qubits. Indeed, they show that such a device would take just eight hours to complete the calculation. “[As a result], the worst case estimate of how many qubits will be needed to factor 2048 bit RSA integers has dropped nearly two orders of magnitude,” they say.
Even the most optimistic anticipation of the advent of quantum computing does not mean that RSA is completely broken and should no longer be used. Not at all. But it does imply that we probably need to think about using longer RSA keys a little earlier than we had originally planned, assuming that we want to continue to use RSA. (It might also be useful to read through the US NIST response to these quantum challenges if you want to research this fascinating topic in further detail).
DNSSEC and Large Key Sizes
Using larger keys in crypto has several implications when we are talking about the DNS. Larger keys mean larger DNS signatures and larger payloads, particularly for the DNSKEY records. A comparison of key sizes and DNSSEC signature record sizes is shown in Table 2.
| Algorithm | Private Key | Public Key | Signature | Security Level (bits) |
| RSA-1024 | 1,102 | 438 | 259 | 80 |
| RSA-2048 | 1,776 | 620 | 403 | 112 |
| RSA-4096 | 3,312 | 967 | 744 | 140 |
| ECDSA P-256 | 187 | 353 | 146 | 128 |
| Ed25519 | 179 | 300 | 146 | 128 |
Table 2 – Crypto Sizes (Bytes)
Larger key sizes also imply that it takes more time to both sign and validate signatures. Table 3 shows the elapsed time taken to sign a zone with 500K entries, using OpenSSL 1.1.1k libraries on a FreeBSD 12.2 host with the DNSSEC toolset supplied with Bind 9.16.16. Validation time is elapsed time for completing 50K queries with DNSSEC validation, and for comparison I’ve included the time taken for the same set of queries into an unsigned zone. The absolute time intervals are not that important here, but the relative differences in time when using the different crypto algorithms and key sizes is important. RSA adds to the signing time at a rate that rises at a higher rate than the key size (i.e. double the key size in RSA takes more than double the time). (Table 3).
| Algorithm | Signing Time (secs) |
Validation Time (secs) |
| Unsigned | 905 | |
| RSA-1024 | 52 | 1,168 |
| RSA-2048 | 126 | 1,173 |
| RSA-4096 | 830 | 1,176 |
| ECDSA P-256 | 159 | 1,036 |
| Ed25519 | 205 | 1,008 |
Table 3 – DNSSEC timings (seconds)
Using RSA with 4,096-bit keys implies taking more time to sign and validate these signatures (although the other overheads associated with fetching the validation records tend to swamp the crypto processing time in this simple experiment). It also implies that DNS responses will be larger. Larger DNS records in UDP means dancing around the issues of IP fragmentation, UDP buffer size settings, truncation of responses and requests via TCP, as we will discuss further here.
Here I’d like to look in detail at how the public DNS infrastructure copes with a zone signed using RSA with 4,096-bit keys. The measurement approach used here is based on an active probing approach by getting most of the Internet’s validating recursive resolvers to validate DNSSEC-signed responses that use RSA-4096 signatures.
When using RSA-4096, the RRSIG records (the digital signatures of the DNS data records) are larger than RRIG records generated by equivalent strength elliptical curve algorithms. In our test case a DNS response to an address query (A or AAAA) with an RSA-4096 signature uses a 747-octet payload, compared to a 195-octet payload when using an ECDSA P-256 signature. While this 747-octet payload is larger than the basic DNS over UDP maximum response size of 512 octets, this doesn’t appear to present any significant issues to DNS resolvers, because most DNSSEC-validating resolvers use a UDP Buffer Size parameter in their queries that is larger than 512 octets. The DS query used in the validation process has a similar response size to the address query, and in our RSA-4096 case the signed DS responses use a 721-octet payload. The DNSKEY query generates a larger DNS response than the A, AAAA and DS records, given that the record contains the RSA-4096 key. In our case this DNS response is 1,263 octets. This DNSKEY response should not present a packet fragmentation issue for DNS over UDP, given the predominate Internet use of a 1500 octet MTU. This size of MTU allows for a maximum unfragmented UDP payload size of 1,472 octets using IPv4 and 1,452 octets using IPv6, which will comfortably carry the signed DNSKEY records without requiring either fragmentation or truncation.
However, there have been some recent changes in the DNS as configured by default by vendors of DNS resolver software. In October 2020 the “DNS Flag Day 2020” program advocated a default setting of the EDNS UDP buffer size to 1,232 octets. This is a highly conservative value, and it was intended to ensure that no UDP packet greater than 1,280 octets in size was sent in DNS over UDP. This value was deliberately calculated to match the maximum assured unfragmented IPv6 packet size of 1,280 octets.
If we put this recommendation of an EDNS UDP buffer size of 1,232 octets together with the requirement to pass a UDP payload of, in our case, 1,263 octets, then the result is that the DNSSEC validation process will take longer, as these large DNSKEY responses over UDP will be truncated. The truncation of the UDP response means that a TCP session will need to be established to re-query for this record. That’s an additional 2 round trip times that have been added to the validation process (one for the TCP handshake and one for the DNS query and response). (Figure 1)
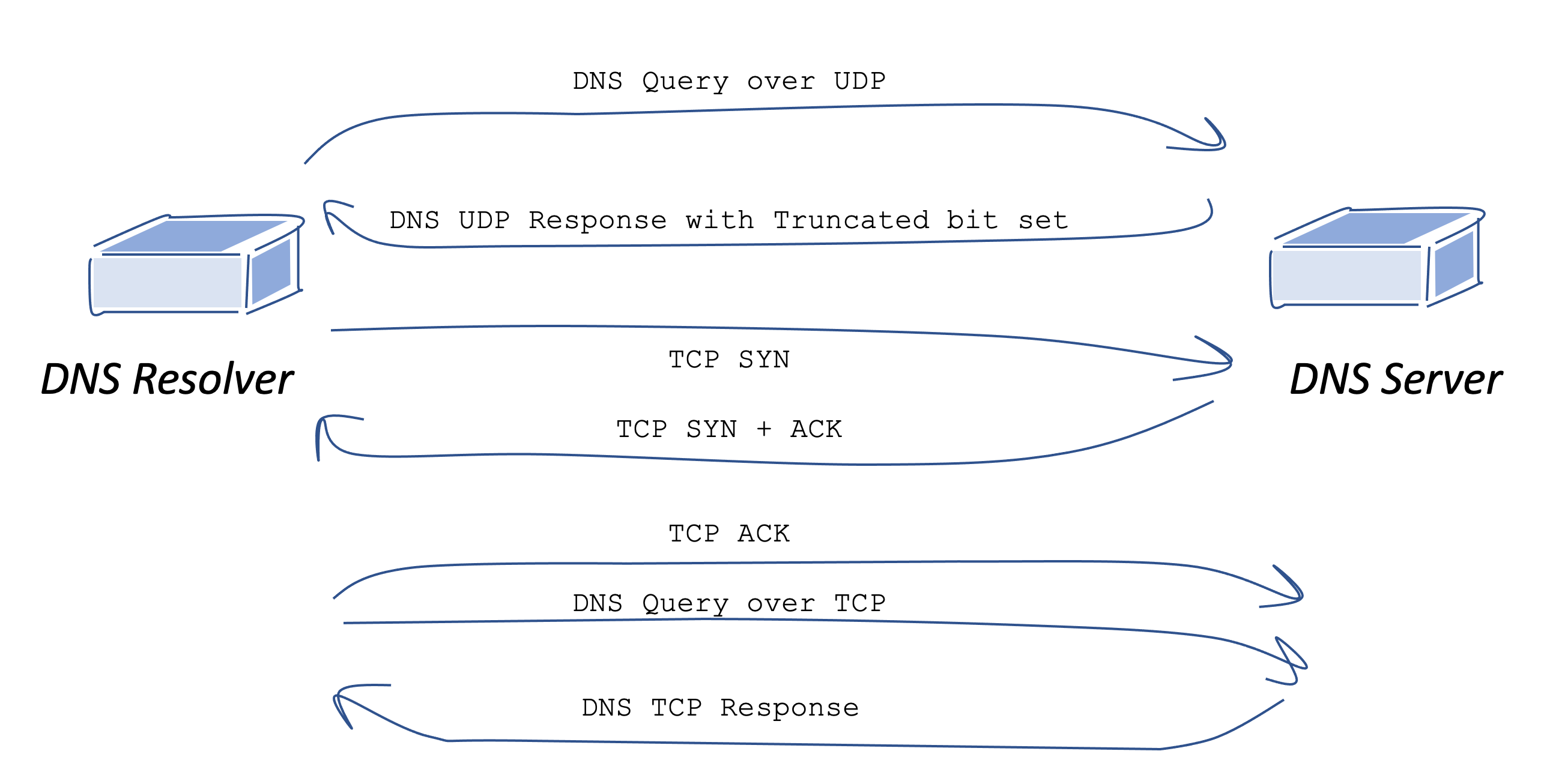
Figure 1 – DNS UDP truncation and re-query over TCP
It’s also the case that previous measurements of the DNS have shown that not every DNS resolver can set up a TCP session, and when such a resolver receives a truncated UDP response then the resolver is wedged and unable to proceed with the query.
So perhaps the first item of data to look at in this measurement of RSA-4096 is the distribution of EDNS UDP buffer sizes used by recursive resolvers in the public Internet. How far has the Internet’s DNS recursive resolver set come in supporting the DNS Flag Day 2020 recommendations? What is the profile of UDP Buffer sizes used in DNS queries by DNSSEC-validating resolvers?
If we look at the distribution of UDP Buffer Size values by query count when used by DNSSEC-validating recursive resolvers when querying for the DNSKEY resource record, we get see a distribution of the values by query as shown in Figure 2.
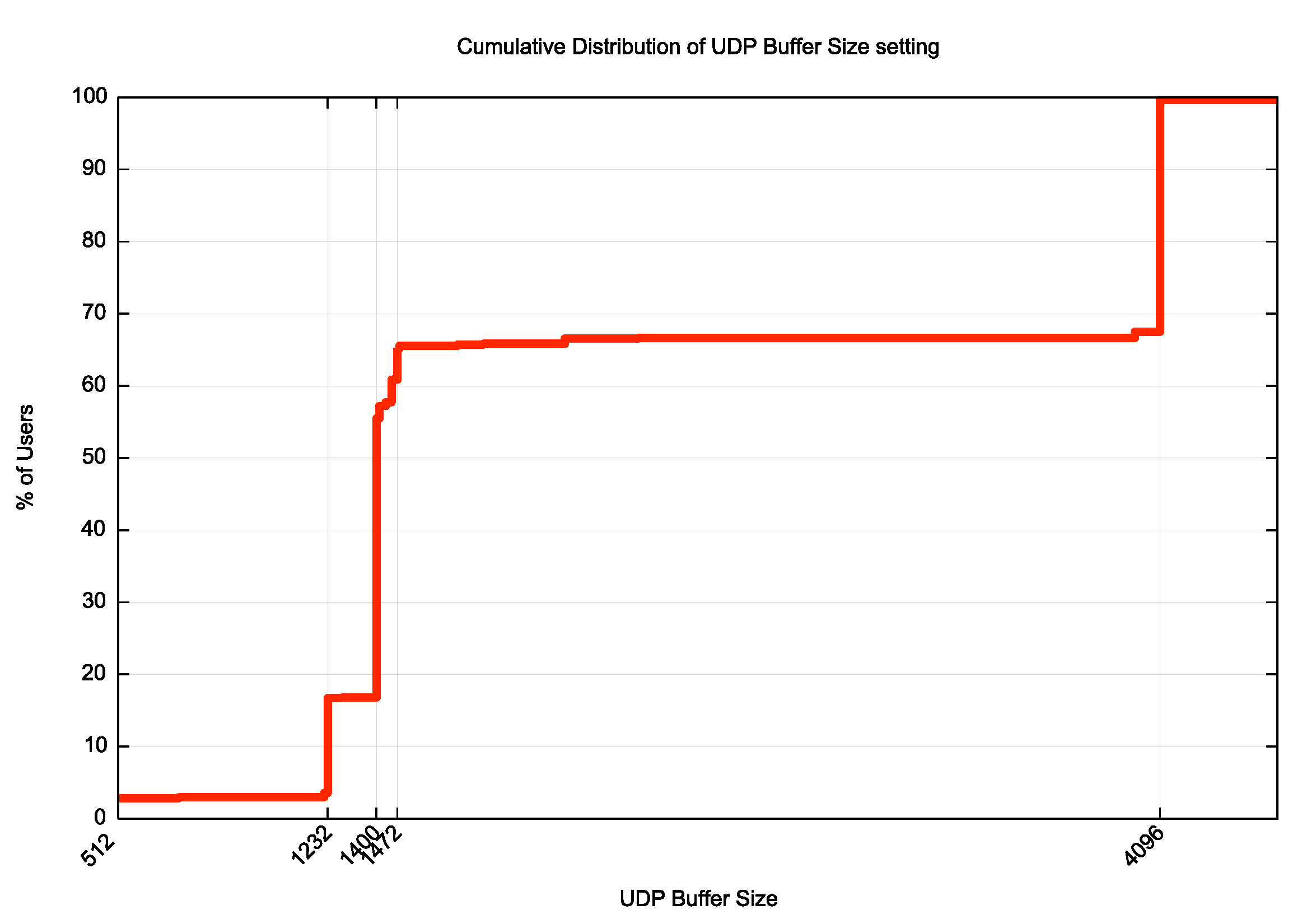
Figure 2 – Distribution of EDNS(0) UDP Buffer Size values by Query
The most common UDP Buffer sizes by query count are shown in Table 4.
| UDP Buffer | % of queries |
| 4,096 | 41.74% |
| 1,400 | 33.82% |
| 1,232 | 9.43% |
| Not Specified | 3.88% |
| 1,472 | 3.05% |
| 512 | 2.52% |
| 1,452 | 1.39% |
| 1,410 | 1.04% |
| 1,220 | 0.72% |
| 8,192 | 0.47% |
Table 4 – Distribution of EDNS(0) UDP Buffer Size values by Query
There has been some recent review of this 2020 Flag Day recommendation, and an internet draft in the DNSOP Working Group of the IETF (https://datatracker.ietf.org/doc/draft-ietf-dnsop-avoid-fragmentation/) recommends a EDNS UDP buffer size of 1,400 octets, which would certainly accommodate the larger responses of DNSKEY records when using RSA-4096 and corresponds with common current practice in DNS resolvers while still avoiding gratuitous truncation and re-query over TCP.
Looking at the DNS always reveals behaviours that one would never think would be possible, as they make no sense to a casual observer. Here is a tcpdump record of a query that was repeated at a high frequency during our measurement:
IP6 2400:c600:1331::.64116 > 2400:8901::.53: DNSKEY? 0di-u312782b8-c19-a5f45-s1630838626-i256fcd4a.ape.dotnxdomain.net.
What’s odd about this query?
It appears that the resolver is assembling a DNSSEC validation chain, and to do so it generates a sequence of queries for the DNSKEY for the current zone and the DS and DNSKEY records for all parent zones up to the root zone. Validation requires that the server also provides the digital signature of these DNSSEC records, so one would expect to see the query include the EDNS(0) option with the DNSSEC OK (DO) bit set to direct the server to include the RRSIG digital signature in the response. And that’s exactly what’s missing from this and a large set of similar queries from this errant resolver!
Of more interest to us in trying to predict the level of TCP re-query is the cumulative distribution of these values, and rather than looking at the data by query let’s look at the distribution of sizes by end user (rather than by query count). This is shown in Figure 3.

Figure 3 – Cumulative Distribution of EDNS(0) UDP Buffer Size values by User
Figure 3 shows that some 16.8% of users (or approximately 1 in 6 users) send their queries to resolvers that have a UDP buffer size of less than 1,263 octets. When the response is larger than 1,263 octets, then they will receive a truncated response over UDP. From this data we would expect that issues with truncation and TCP re-query would only be visible in at most some 16% of cases when using a RSA-4096 key.
Given this background in query behaviour and profiles of UDP buffer sizes in queries, lets now move on to looking at the results of this measurement experiment.
Measurements of RSA-4096
The test was conducted using an online ad campaign to enrol an Internet-wide sample of end users into the test. The test consists of a small set of URLs to fetch, using unique DNS names in the URLs to ensure that the DNS resolution cannot use previously cached DNS information.
DNSKEY with 1 x RSA-4096 Key
Let’s look at the results when we use a test with a DNSKEY record that contains a single RSA-4096 key, which corresponds to a DNS payload of 1,263 octets. We use a control test as a comparative indicator. This control is that of a DNSKEY record with a single RSA-1024 key, where the signed response is 491 octets in length, which fits within the default DNS maximum payload size of 512 octets. The results are shown in Table 5, where the percentages shown in the table are percentages of test cases (or “users”).
| Algorithm | Validating | Mixed |
| RSA-1024 | 29.7% | 9.0% |
| RSA-4096 | 29.4% | 9.1% |
Table 5 – Comparison of DNSSEC Validation outcomes between RSA-1024 and RSA-4096
These measurements were gathered across 7-day intervals in September 2021.using different sets of end-clients to test each crypto algorithm profile, with an average sample size of some 5.5M individual experiments for each algorithm profile.
The Validating response column in Table 5 is where the user’s stub resolver is located behind one or more DNSSEC-validating recursive resolvers, all of which perform DNSSEC validation. Here a validly signed DNS name will be successfully resolved, while an invalidly signed DNS name will fail resolution. We can detect this DNS resolution failure through a failure to retrieve the web object referenced by the test URL.
In the Mixed case there is at least one recursive resolver in the end user’s configured resolver set that does not perform DNSSEC validation, in which case the invalidly signed DNS name will successfully resolved for the end user, and the reference web object will be fetched by the user.
The differences here between the two RSA key sizes is quite subtle, with a drop of just 0.3% of Validating clients with the larger 4096-bit key, and a rise of 0.1% of Mixed validating clients. The differences are most likely to be caused by the onset of UDP truncation and lower reliability of TCP re-query with the larger key, although these differences are sufficiently low as to fall within the parameters of experimental uncertainty, so this interpretation of the results is speculative.
We have already noted that in terms of the observed DNSSEC validation queries some 16% use a UDP buffer size of 1,263 or less, so we should expect a visible proportion of validation query sequences to generate truncated UDP responses when resolving the DNSKEY RR with RSA-4096. And this is what we observed here (Table 6).
| UDP | x-UDP+TCP | x-UDP | |
| RSA-1024 | 100% | 0% | 0% |
| RSA-4096 x 1 | 74% | 23.5% | 2.5% |
Table 6 – UDP and TCP use – RSA-4096 single key
In terms of the sequence of queries associated with name validation DNS query/response sequences, 74% of these cases that perform DNSSEC validation with RSA-4096 do so using only UDP. A further 23.5% of experiments had a truncated UDP response and a successful TCP re-query. In 2.5% of experiments the truncated UDP response was not followed up by a TCP query, and the entire validation process failed within this resolver, and it returned a SERVFAIL response code to the stub resolver. In most of these cases it appears that the stub resolver was able to re-query using a recursive resolver which either performed validation with a larger UDP buffer size in its queries or did not perform validation at all. In either case the initial truncated UDP response did not elicit a TCP re-query. It appears that recursive resolvers that have set their UDP buffer size to a value less than 1,263 octets appear to be relatively robust in terms of the reliability of the TCP re-query, and in those cases where this has not occurred, the stub resolver generally has options to re-query using a different recursive e resolver.
As the RSA-1024 response is 491 octets it fits within the DNS-defined 512 octet payload size, and no responses were truncated, so there are no issues with the reliability of a failover to TCP as this does not occur in this context.
DNSKEY with 2 x RSA-4096 Keys
This measurement is not entirely the complete picture in terms of measuring the viability of RSA-4096 keys in DNSSEC. It is not all that common to use the same key as both the zone signing key (ZSK) that signs the zone’s resources records and the key signing key (KSK) that is signed by the parent in the Delegation Signer (DS) record. A more common operational practice is to separate these roles and use the KSK as the key that is secure entry point that signs only the DNSKEY record, and use a separate ZSK to sign all the other entries in the zone. There is not much that changes with this model except for the zone’s DNSSEC resource record. With distinct KSK and ZSK keys, the DNSSEC record now contains two RSA 4096-bit keys, together with the digital signature. The size of this DNSKEY record when using RSA-4096 as the crypto algorithm is 1,755 octets. This makes for a larger DNS response and entails either UDP fragmentation or DNS over UDP truncation and re-query in TCP to complete the validation function, as the DNS responses in both IPv4 and IPv6 exceed the server’s MTU of 1,500 octets.
Table 7 looks at the relative level of TCP used by DNSSEC-validating resolvers based on a count of DNS validation tasks generated by this experiment using 2 x 4096-bit keys, measured over a 7-day period in September 2021.
| UDP | x-UDP+TCP | x-UDP | |
| RSA-1024 | 100% | 0% | 0% |
| RSA-4096 x 1 | 74% | 24% | 2% |
| RSA-4096 x 2 | 47% | 50% | 3% |
Table 7 – UDP and TCP use
In one half of the cases where the DNS response is validated the resolver is passed a fragmented UDP response. In 46% of cases the resolver is passed a UDP response that has been truncated and then the resolver re-queries using TCP. In the remainder of cases there is no successful TCP re-query and the user appears to re-query using a different recursive resolver to validate the DNS response. This TCP failure case is most likely due to local security policy settings that restrict resolver traffic to DNS queries to UDP port 53 only. In this case the resolver will be unable to progress with the validation and it will stop at this point and return a SERVFAIL response code to the client’s stub resolver, which will then, in turn, re-query using another recursive resolver, if that has been configured at the client.
If we can measure the incidence of this situation where the truncated UDP response cannot be resolved by the recursive resolver using TCP, nor are there working alternative recursive resolvers available for the stub resolver, we can measure the extent to which this large DNS payload is causing resolution failure due to failure to validate the response. If we look at the DNSSEC validation rate in this case, the average validation rate falls from 29.4% of users with a single RSA-4096 key to 27.9% with two RSA-4096 keys.
| Algorithm | Validating | Mixed |
| RSA-1024 | 29.7% | 9.0% |
| RSA-4096 x 1 | 29.4% | 9.1% |
| RSA-4096 x 2 | 27.9% | 9.6% |
Table 8 – Comparison of Validation outcomes
There are two issues going on here that contribute to this 1.5% decline in Validation rates for the larger DNSKEY record. The first concerns resolvers that are using a large UDP buffer size in their queries (larger than 1,755 octets). This is the case for some 34% of users. If the resolver is incapable of receiving and reassembling a fragmented UDP packet, then the resolver necessarily times out in waiting for a response to its query. Older versions of DNS resolver software performed a re-query in such cases using smaller UDP buffer sizes, but this behaviour has largely been replaced with a SERVFAIL response, allowing the stub resolver the option to query using a different recursive resolver. The second issue concerns the small proportion the other 66% of users, who receive a truncated DNS response over UDP and are unable to complete the subsequent TCP re-query.
DNSKEY with 3 x RSA-4096 Keys
This 2-key DNSKEY situation is not quite the final word here. There are a number of scenarios when rolling a DNSSEC key where the old key is used to sign across the incoming key and subsequently the keys are swapped, and the old key is removed. This allows a key to be rolled while still preserving the integrity of the signed zone and allowing caching resolvers to maintain a coherent view of the zone’s keys and signatures through the rollover process (see RFC7583 for more details on the timing of such a staged-key keyroll process). This process entails a period where there are three keys in the DNSKEY record, assuming the KSK and ZSK keys are rolled independently. Let’s look at how well this 3-key situation is managed when using RSA-4096 keys.
In this case the signed DNSKEY RR contains 3 keys and a signature, and the total size of the DNS response is 2,299 octets with RSA-4096 keys. This should be similar to the 2-key situation, given that there is a 0.3% difference in the number of clients using resolvers with a UDP buffer size setting of 1,755 octets or greater and a setting of 2,299 octets (Table 9).
| Algorithm | Validating | Mixed |
| RSA-1024 | 29.7% | 9.0% |
| RSA-4096 x 1 | 29.4% | 9.1% |
| RSA-4096 x 2 | 27.9% | 9.1% |
| RSA-4096 x 3 | 24.0% | 7.8% |
Table 9 – Comparison of Validation outcomes
Unexpectedly, the larger DNSKEY response appears to cause issues for 3.9% of clients who are Validating clients, and 1.2% of clients who use a mix of validating and non-validating resolvers.
| UDP | x-UDP+TCP | x-UDP | |
| RSA-1024 | 100% | 0% | 0% |
| RSA-4096 x 1 | 74% | 24% | 2% |
| RSA-4096 x 2 | 47% | 50% | 3% |
| RSA-4096 x 3 | 47% | 50% | 3% |
Table 10 – UDP and TCP use
The UDP truncation and TCP behaviour are very similar across these two cases (Table 10).
Why is there a change in both the Validating and Mixed cases when the distribution of UDP buffer size values in queries suggests that we would see a similar outcome in these cases?
A possible factor concerns the recursive resolver’s handling of fragmented IP packets. According to the still current IPv4 IP standard, RFC791, all IPv4 hosts must be capable of reassembling an IP datagram of total size up to 576 octets and may silently discard larger datagrams. In IPv6 a similar upper limit of a mandatory-to-support size of the fragmentation reassembly function is 1,500 octets, and an IPv6 host may silently discard a datagram whose reassembled size is greater than this size. Both the 1,755-octet and 2,299-octet DNS payloads in a UDP packet exceed these basic IP parameters of assured reassembly.
However, this is an unlikely factor, in that most implementations of the IP protocol do not have a per-packet IP reassembly limit but define a maximum amount of memory that is used to hold all partially reassembled packets.
More likely is the existence of security filter rules at the resolver that are likely to classify a large DNS response as part of a DOS attack. In this case “large” may well be around the 2,048-octet level for the DNS payload, leading to the higher drop rate for the larger 3-key case.
Variations by Economy and Network
Global averages mask out a lot of detail, and when we look at the same data using geo-location information to map the tested end points into countries, we can see those economies where the change in validation outcomes between RSA-1024 and RSA-4096×2 is the greatest.
| RSA-1024 | RSA-4096×2 | Difference | |
| Portugal | 68% | 40% | -28% |
| Morocco | 59% | 31% | -27% |
| Iceland | 95% | 72% | -23% |
| Guyana | 41% | 28% | -13% |
| USA | 60% | 48% | -12% |
| Ireland | 27% | 18% | -9% |
| Switzerland | 81% | 73% | -9% |
| Brunei | 31% | 23% | -8% |
| Singapore | 71% | 64% | -8% |
| Sweden | 91% | 84% | -7% |
Table 11 – Validation Rates across RSA key sizes by Economy
Similarly, we can map the test points into the associated host network and list those networks where we have gathered sufficient results to have a meaningful reading, and where the difference between RSA-1024 and RSA-4096×2 is the greatest.
| RSA-1024 | RSA-4096 x 2 | Difference | AS Name | |
| AS39603 | 93% | 47% | -45% | P4 UMTS, Poland |
| AS5466 | 94% | 51% | -44% | Eircom, Ireland |
| AS23688 | 93% | 54% | -39% | Link3, Bangladesh |
| AS45543 | 73% | 34% | -39% | SCTV, Vietnam |
| AS36903 | 77% | 41% | -36% | MT-MPLS, Morocco |
| AS34779 | 91% | 56% | -35% | T-2, Slovenia |
| AS35819 | 93% | 65% | -28% | Etihad Etisalat, Saudi Arabia |
| AS28573 | 63% | 37% | -26% | Claro, Brazil |
| AS3243 | 92% | 67% | -25% | Meo Residencial, Portugal |
| AS4818 | 91% | 69% | -22% | Digi Telecom, Malaysia |
Table 12 – Validation Rates across RSA key sizes by AS
Presumably the resolvers located in this network have some form of drop filter applied to DNS over TCP, or more likely, some filter that applies a maximum size to DNS responses as a defence against DNS-based DOS attacks.
Conclusions
The DNS must steer a careful path between two problem areas. If the recursive resolver uses a large UDP buffer size then it may encounter the issue of IP fragmentation loss, which causes the querier to encounter a timeout on the query. If the UDP buffer size is set to the anticipated MTU size, less the IP and UDP packet headers of course, then it will receive a truncated UDP response and then must re-query over TCP. In this case the response takes more time, and the resolver may still encounter the issue of network-based TCP blocking.
In the case of RSA with 4,096-bit keys we see DNS resolvers encountering these issues. The relative incidence is, at a whole-of-Internet level of the order of 2% – 3% of users, but there are individual networks where these issues are clearly evident at a much higher rate. The compounding factor here is that a failure to resolve a name because of a validation failure will result in the DNS outcome being withheld from the stub resolver. From that perspective it certainly appears that RSA with 4,096-bit keys is a step too far, and alternatives should be considered.
In other words, these measurements suggest that using RSA with 4,096-bit keys in the DNS is not a practical choice in terms of the resilience of validating DNS resolvers being able to handle this configuration.
How do we avoid these pitfalls of signing DNS records with RSA using 4,096-bit keys?
One answer is to avoid using large RSA keys. In this case RSA with 4,096-bit keys encounters a visible level of resolution failure, due to the inconsistent handling of the larger DNS responses for the DNSKEY record, and the current practice appears to point to the use of 2,048-bit keys as a suitable security choice for the moment. The problem is that the crypto environment is a moving target and over time smaller RSA keys will be more vulnerable as we develop more capable computers.
Another answer is to use a “denser” crypto algorithm that has a high security level with a far smaller key size than RSA. Here the Elliptical Curve algorithm, ECDSA P-256, is an obvious contender, and in our next article that looks at DNSSEC algorithms. I’ll compare ECDSA P-256 and RSA in terms of the level of support for these algorithms in today’s DNS.
The Edwards Curve family of algorithms has a similar crypto density to Elliptical Curve algorithms, but the problem with using such algorithms such as Ed25519 for DNSSEC signing, is that the level of acceptance of this algorithms in validating resolvers is still well below ECDSA (see this report for details of recent measurements of this comparison).
However, it should be noted that this “security level” relates to conventional non-quantum computers and algorithms. Our current thinking about quantum computers is that some algorithms appear to be more “quantum-resilient” than others, and specifically RSA with larger keys will be more resilient than an equivalent strength elliptical curve profile in this envisaged quantum environment.
Afterword: Secure Lifetimes, DNSSEC and the DNS
This article started with some consideration of the topic of the anticipated secure lifetime of a piece of ciphertext, noting that when choosing an encryption algorithm, the choice needed to take into account the anticipated changes in computational capacity over this secure lifetime.
It is useful to ask whether this is a relevant consideration for DNSSEC. In choosing an algorithm to sign a DNS record should we be concerned about the secure lifetime of this digital signature?
DNSSEC is not used to encrypt DNS data. From the perspective of DNSSEC, DNS data is public data and DNSSEC does not help at all to protect its secrecy. There are other mechanisms to provide channel security for DNS queries and responses (DNS over TLS, DNS over QUIC, and DNS over HTTPS) and other mechanisms to pull apart the association of who is making what DNS query (oblivious DNS). DNSSEC protects the data against tampering and a more limited protection against replay of stale DNS data.
This consideration implies that secure lifetime of a data item secured by a DNSSEC signature is based on the lifetime of the key that signs the data lifetime. The more frequently a zone admin rolls the keys, and the shorter the signature validity periods the shorter the window available for an attacker to crack the algorithm and manufacture bogus DNS records that appear to be validly signed.
This then gives zone administrators a trade-off in terms of anticipated secure lifetimes for their choice of crypto algorithm profiles. More secure keys have a longer anticipated secure lifetime, but the longer DNS records may cause DNS failures. If the keys are rolled regularly, then the window of opportunity for attack is shortened, and the secure lifetime need only be of the same order of length as key lifetimes in the zone. This would allow the continued use of key profiles that have a secure lifetime much shorter than 10 years. In this latter scenario the choice of a shorter key also places an obligation on the zone administrator to perform regular a keyrolls within the selected design parameters so sure that an attacker does not have sufficient time to break the encryption profile for each iteration of the key value.
In the case of the Root Zone, the ZSK’s DNSSEC Practice Statement specifies a key lifetime of 3 months, and the KSK’s statement specifies 5 years.