For some years at APNIC Labs we have been conducting measurement experiments concerning the extent of use of IPv6 using a technique of embedding the measurements within the advertisement using Adobe Flash. The results of this measurement are fed into a set of measurement web resources at http://stats.labs.apnic.net/ipv6.
The use of Adobe Flash as a scripting tool for the measurement system behind the online advertisement delivery system has always been somewhat of a compromise, in that we’ve been aware that not all systems support Flash, but at the time HTML5 was still in its early days. In the middle of June we added a second advertising stream using HTML5 as the scripting language for the Ad to augment the existing Flash stream, and in this article we’ll look at the changes this has meant to the data concerning the level of deployment of IPv6 as a result.
What both the Flash and the HTML5 code does is to generate up 3 unique URLs to fetch: a IPv4 only URL, an IPv6 only URL and a Dual Stack URL. If the browser executing the script is capable of fetching one of these IPv6 URLs using IPv6 then we call the host system “IPv6 Capableâ€. If it uses IPv6 to fetch the dual stack URL we call it “IPv6 Preferredâ€.
The first plot is the total number of completed measurements per day (Figure 1). The HTML5 advertisement was introduced on the 16th June, and the first full day of operation was on the 19th June. The HTML5 system uses 3 servers. For the period 25th June – 28th June one of three servers was offline, and over this period the Flash ad rate declined from around 1.75M measurements per day to 1.1M measurements per day. The HTML5 system is currently running at over 2M measurements per day. The Flash-based measurement stream has been slowing dropping in volume over this period, from some 1.5M completed measurements per day at the start of May to a current level of some 1.0M measurements per day.
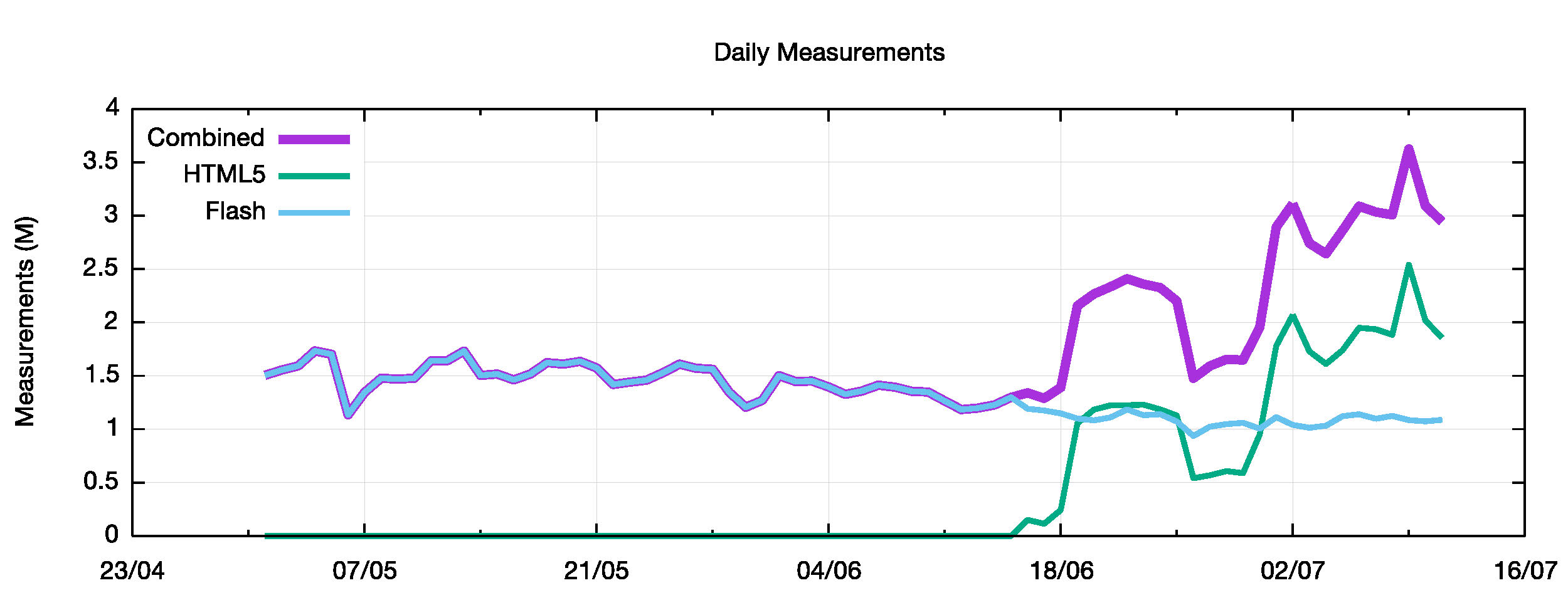
Figure 1 – Total measurements per Day
For each day’s measurements the individual measurements are weighted to compensate for the Advertising network’s presentation bias. (The Advertisement delivery system tends to present the advertisement in a non-uniform manner, so that there are higher per internet user Advertisement presentation rates in some countries over other countries. As part of our processing we attempt to compensate for this by calculating an “ideal†presentation profile and weighting the actual measurements to bring them into alignment with this ideal profile.) The rules described above are used to classifying each end system according to whether it cannot retrieve a IPv6 URL, or it is IPv6 Capable, or it is IPv6 Preferred. The result of this processing and classificaption for the period 12st May to the 10th July is shown in Figure 2.

Figure 2 – Daily Proportions of IPv6 Capable and Preferred
There has been a steady growth in both the IPv6 Capable and Preferred levels over this period, but the period since the 18th June shows a wider gap between the Capable and Preferred measurements. The question we’ve been asked is: “Why has the percentage of IPv6 Preferred systems not risen at the same rate as IPv6 Capable systems?†We’ll spend some time to look at recent data to provide a detailed answer to this question.
Measuring the Change
How “large†is this recent change? There are proportionally a larger number of systems that are IPv6 capable, but prefer to use IPv4 when confronted with a dual stack object to fetch. This difference between IPv6 Capable and IPv6 Preferred (which corresponds to a behaviour where the system is capable of using IPv6, but prefers to use IPv4 if given a choice) is shown in Figure 3. This figure clearly shows a rise in the relative incidence of these systems from 0.4% to approximately 1% when the HTML5 measurement came online.

Figure 3 – Proportion of IPv6 Capable but not Preferred
This graph in Figure 3 strongly suggests that there has been a tangible change associated with the addition of the HTML5 measurements, and this involves the introduction of a set of behaviours that are capable of using IPv6, but do not prefer to use it in dual stack contexts.
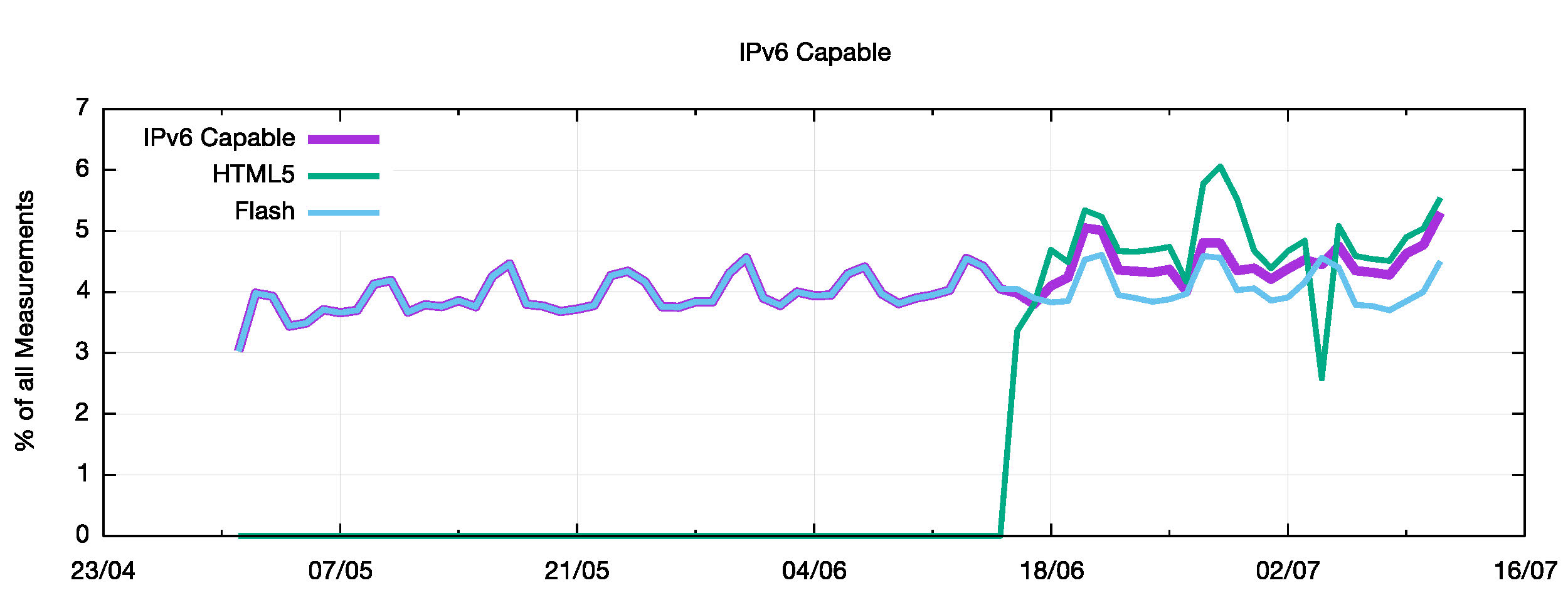
Figure 4 – IPv6 Capable by Advertisement Type
This is also subtly evident in Figure 4, which shows that the level of IPv6 Capable systems detected by the HTML5 script is up to 1.5% higher than that detected by the Flash script.
This change does not appear to be the case for IPv6 Preferred systems, where the behaviours seen by the Flash script are closer to that seen with the HTML5 script, with daily HTML5 numbers of IPv6 Preferred systems being both higher and lower than their Flash-measured counterparts (Figure 5).
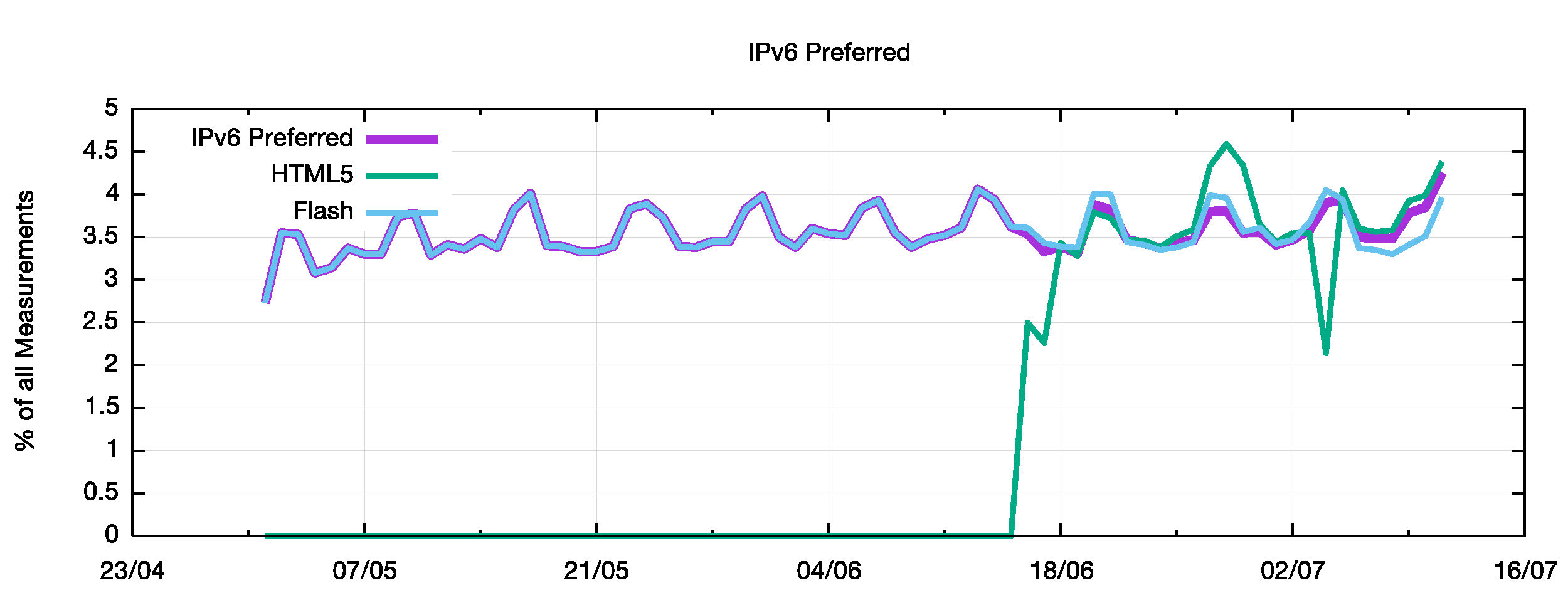
Figure 5 – IPv6 Preferred counts by Advertisement Type
The next step is calculating how much more IPv6 we pick up in HTML5 – this is the difference between the HTML5 and Flash numbers per day. Figure 6 shows that for those systems that are capable of using IPv6, the HTML5 measurement flow sees an additional 1% of end systems per day, while for the systems who prefer to use IPv6 the number is between 0% and 0.5% per day.
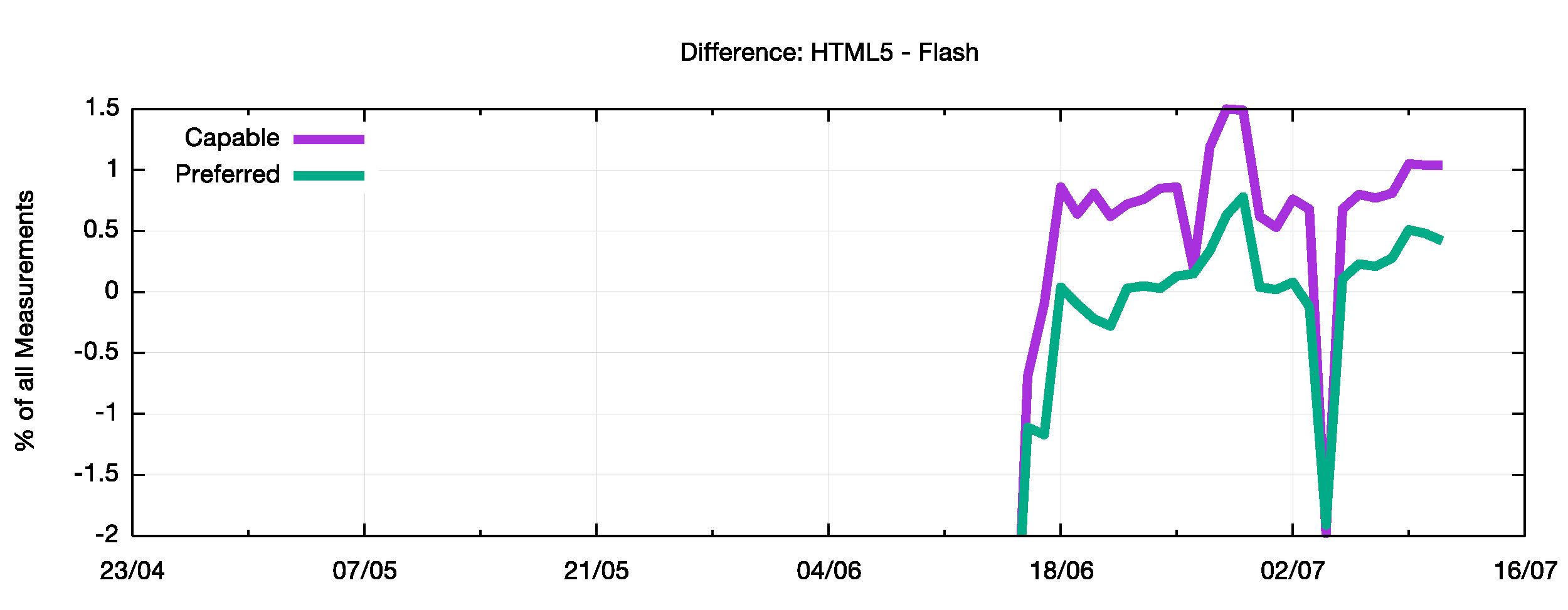
Figure 6 – Difference between HTML5 and Flash IPv6 measurements
System Types
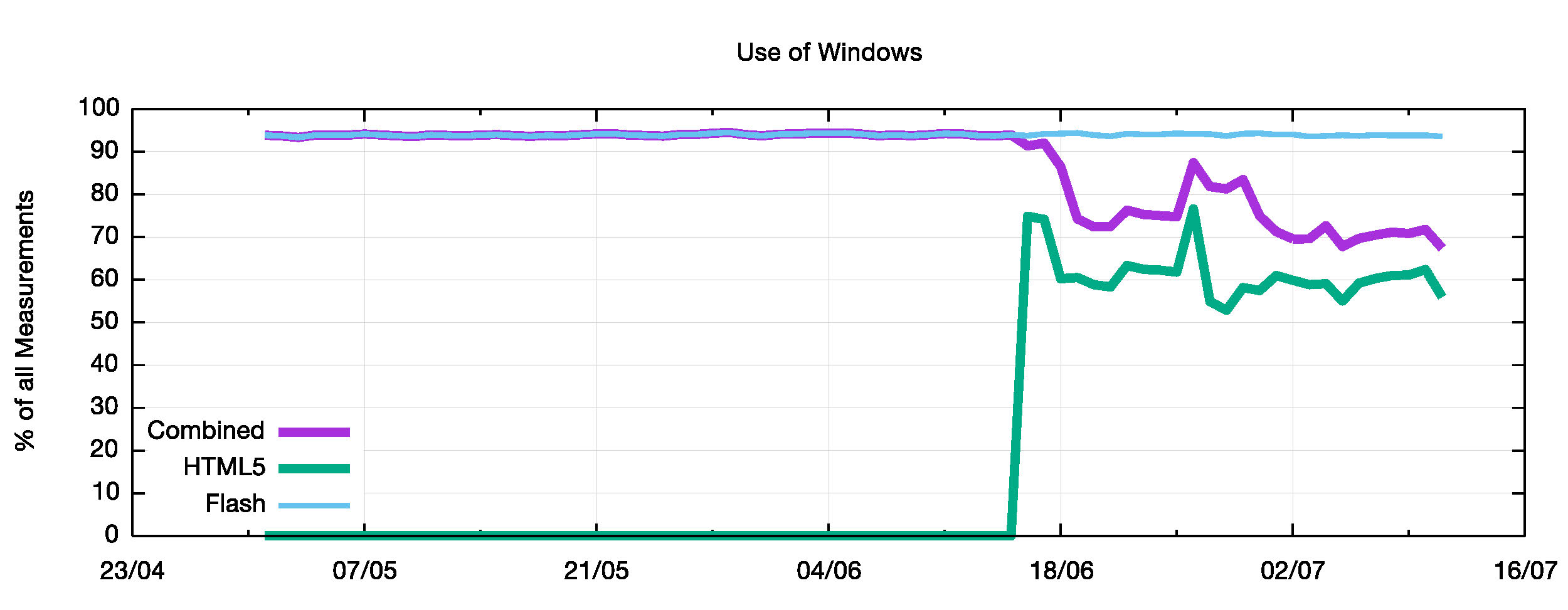
In searching for reasons for the change its useful to look at the collection of systems that are responding to these Advertisements. Let’s look at the measurements and use the Operating System family, as inferred by the browser signature captured in the server’s web logs, and the distinguishing feature. Firstly, let’s look at the Windows family of systems. Figure 7 compares the relative share of Windows systems between Flash and HTML5. While some 95% of systems that respond to Flash are running Windows, this proportion drops to slightly less than 60% of systems that respond to HTML5. Obviously this is a significant change between the two measurement flows.
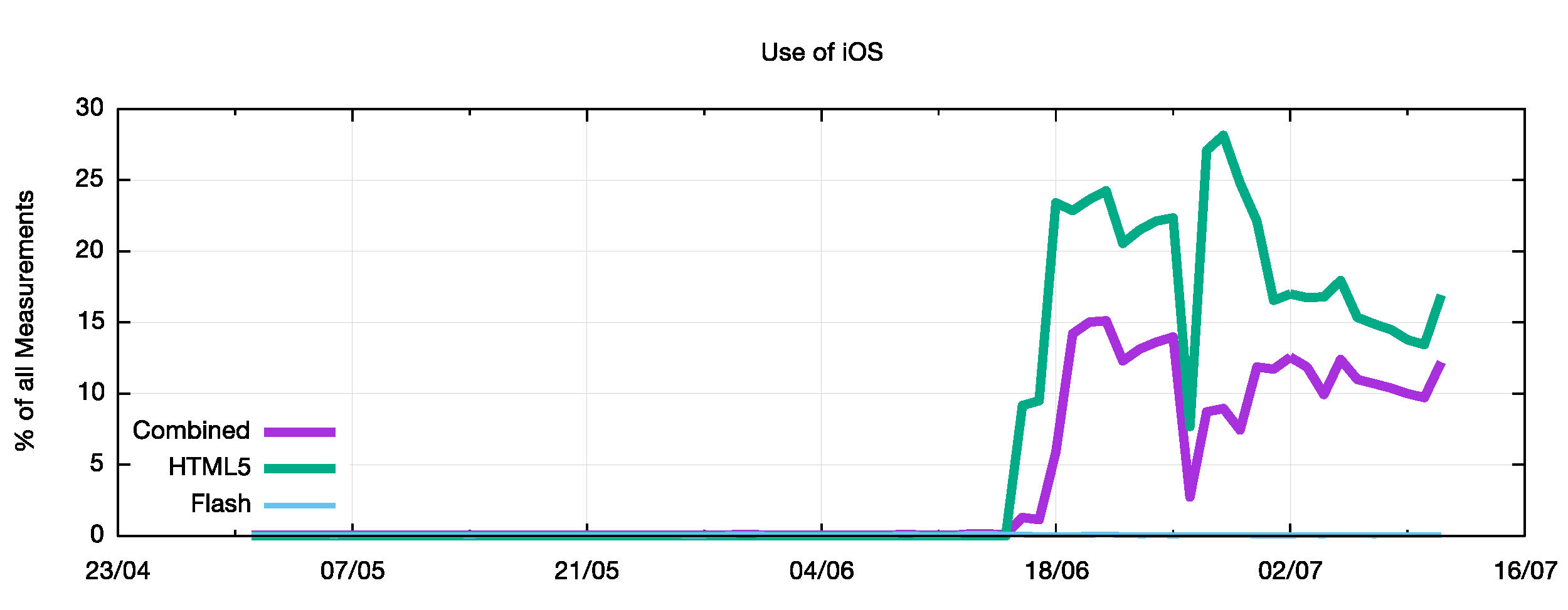
The opposite picture can been seen for Apple’s iOS systems (iPhones and iPads), where virtually no iOS devices respond to Flash, while 15% of systems that are responsive to HTML5 are iOS platforms (Figure 8). Apple does not bundle Flash with the operating system in its iPhones or iPads, so its not surprising to see very few iPhones responding to an advertisement delivered via Flash. It’s a different story using HTML5, and iPhones are capable of responding to HTML5 delivered Ads.
The other major mobile platform OS is Android, and this too is largely unresponsive to Flash, while 22% of systems that respond to HTML5 are Android platforms (Figure 9). The combination of these two measurements imply that while the Flash measurement system is largely incapable of measuring commonly used mobile devices, the HTML5 measurement allows us far better insight into IPv6 use in both mobile devices and mobile networks.
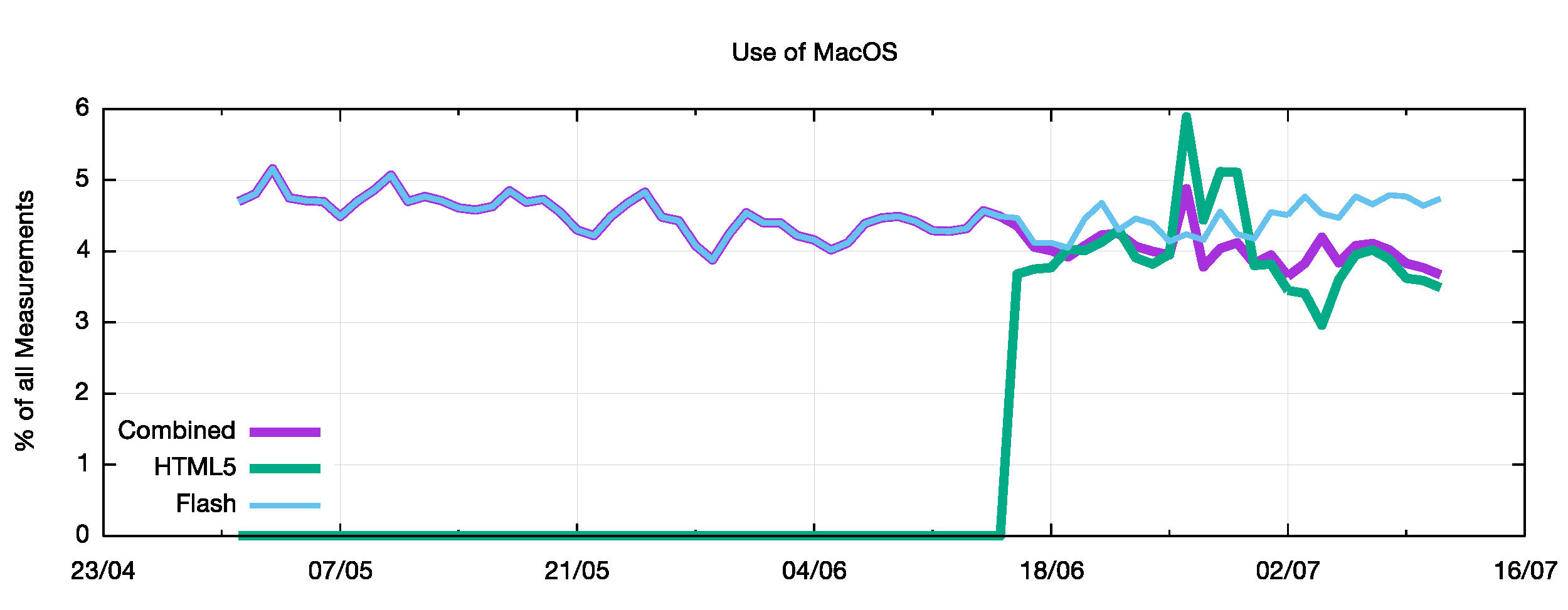
The last of the major platforms in use today is Apple’s Mac OS. Some 4.5% of systems that responded to the Flash Ad were Mac OS systems, while this number dropped to 3.5% for the HTML5 Ad.
It appears that the 35% drop in the relative incidence of Windows platforms from Flash to HTML5 is taken up by a 20% rise in the number of Android platforms and a 15% rise in the number of responding iOS platforms, a change that corresponds to an expansion of the measurement system into mobile networks and devices.
IPv6 Capable and Preferred Behaviours
Do we see any change in IPv6 behaviour between Flash and HTML5 if we look at the numbers per OS platform? Firstly, Windows.
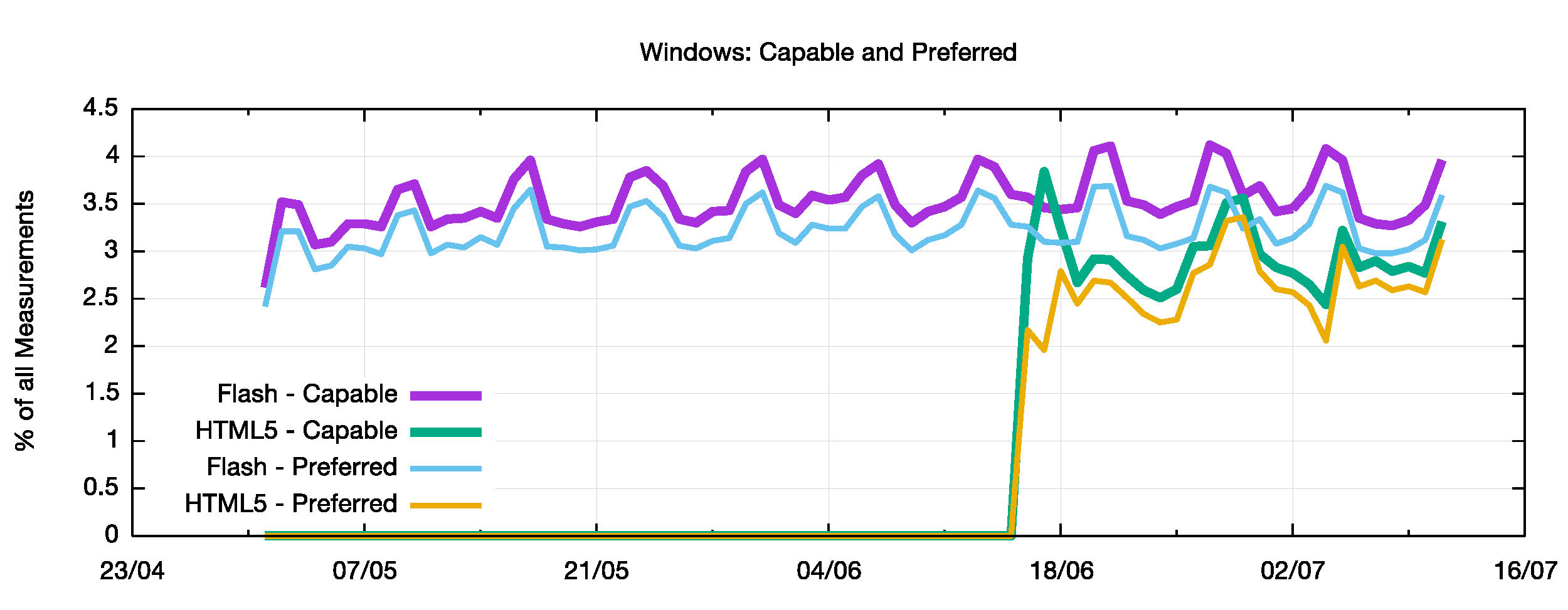
Figure 11 – Preferred and Capable IPv6 for Windows
Approximately 90% of those Windows systems that are capable of using IPv6 will prefer to use IPv6 (It should be noted here that we have removed from the sampling those end systems that use Window’s auto-tunnelling IPv6 mechanisms, 6to4 and Teredo.) This relative difference between Capable and Preferred is maintained in the HTML5 measurement experiment, but the relative number of IPv6 capable Windows platforms has fallen by slightly over 1%.
When looking at a comparable picture for iOS devices there is also a relative drop in measured IPv6 capability from Flash to HTML5. What this graph does not show is that the numbers of responding systems in Flash that report iOS are extremely small (less than 1% of all responding systems per day) while the number of responding systems in HTML5 is some 15% of all systems. Compared to a world average of around 4% of systems that are IPv6 capable, the 8% figure reported by iOS is certainly far higher than the average. The Preferred value is some 60% of the capable figure for iOS.
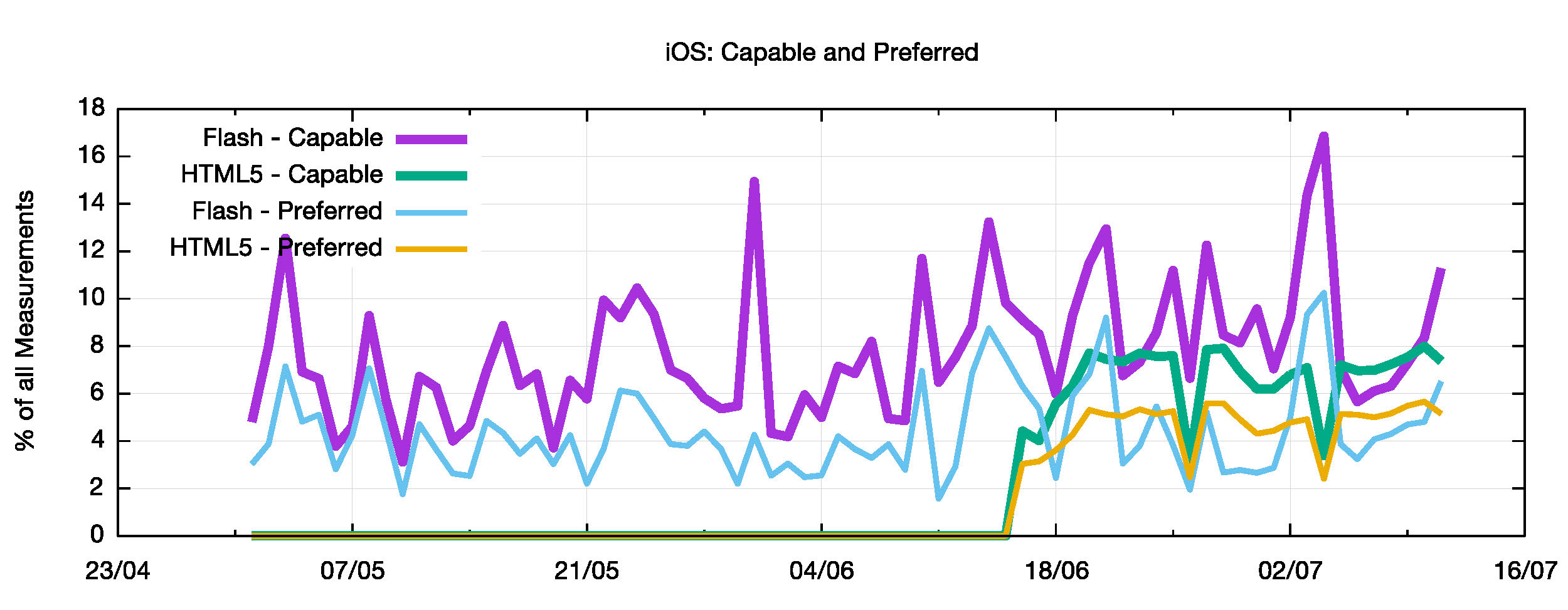
Figure 12 – Preferred and Capable IPv6 for iOS
The Android numbers look anomalous until you take into account that before the 18th June there were almost no android measurements, and after the 18th June almost all of the measurements were HTML5.
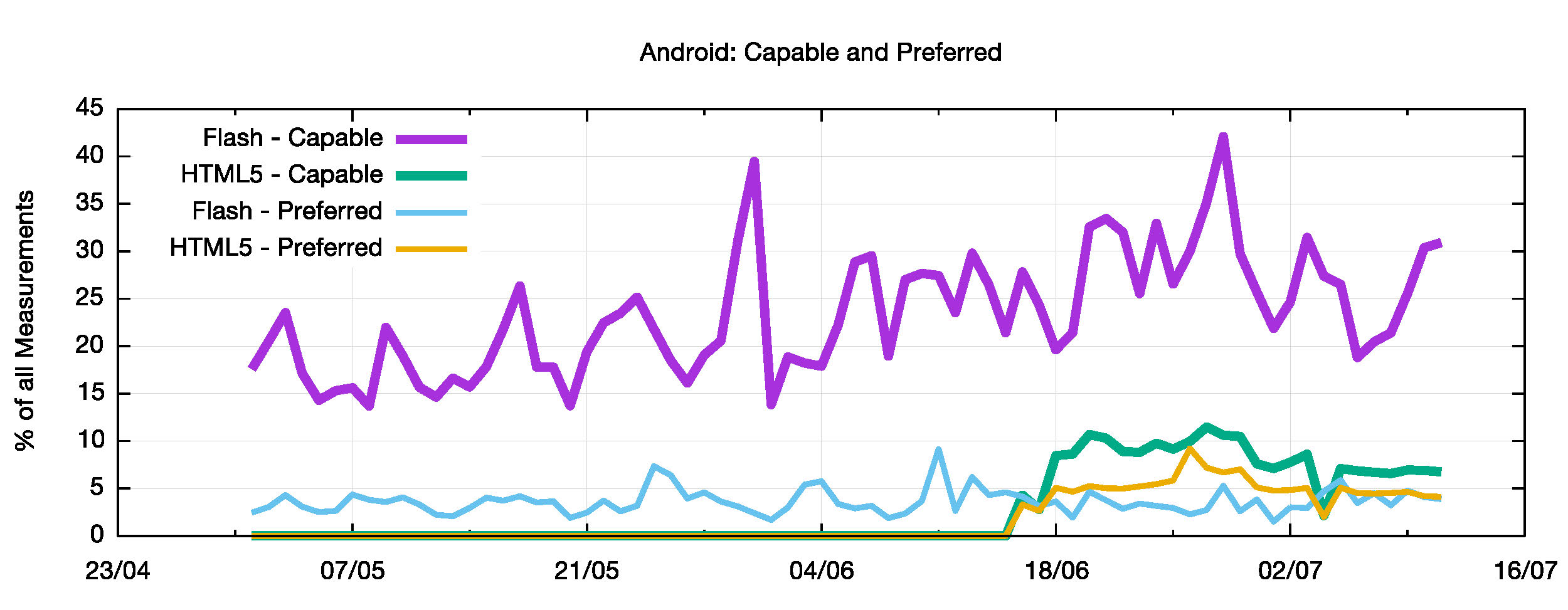
Figure 13 – Preferred and Capable IPv6 for Android
The picture for Mac OS is very similar to that of iOS.
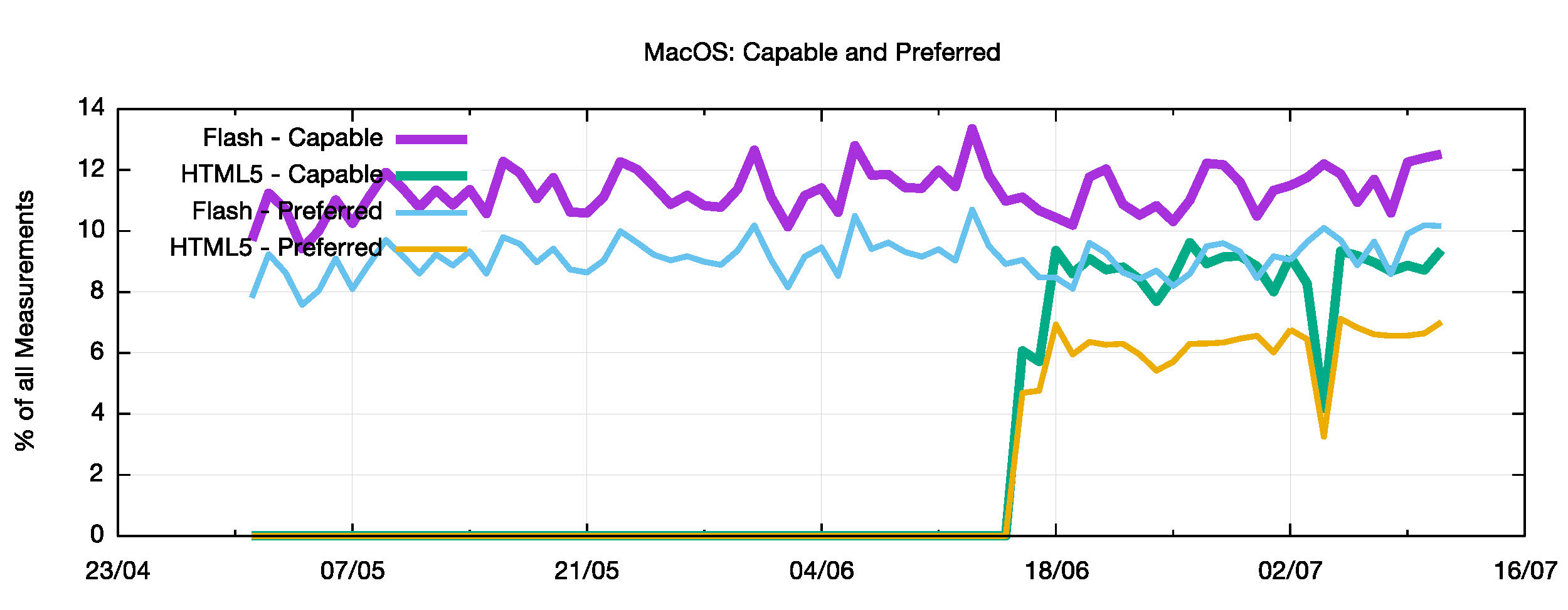
Figure 14 – Preferred and Capable IPv6 for MacOs
Finally, lets look at the ratio of Preferred to Capable for each of the OS families. If the systems have a strong bias to use IPv6 when and if they can, this ratio will approach 1, and when they essentially make a random choice we would expect to see a value of 0.5.
Figure 15 shows the ratio of preferred to capable for those systems that are responsive to the HTML5 Ad.
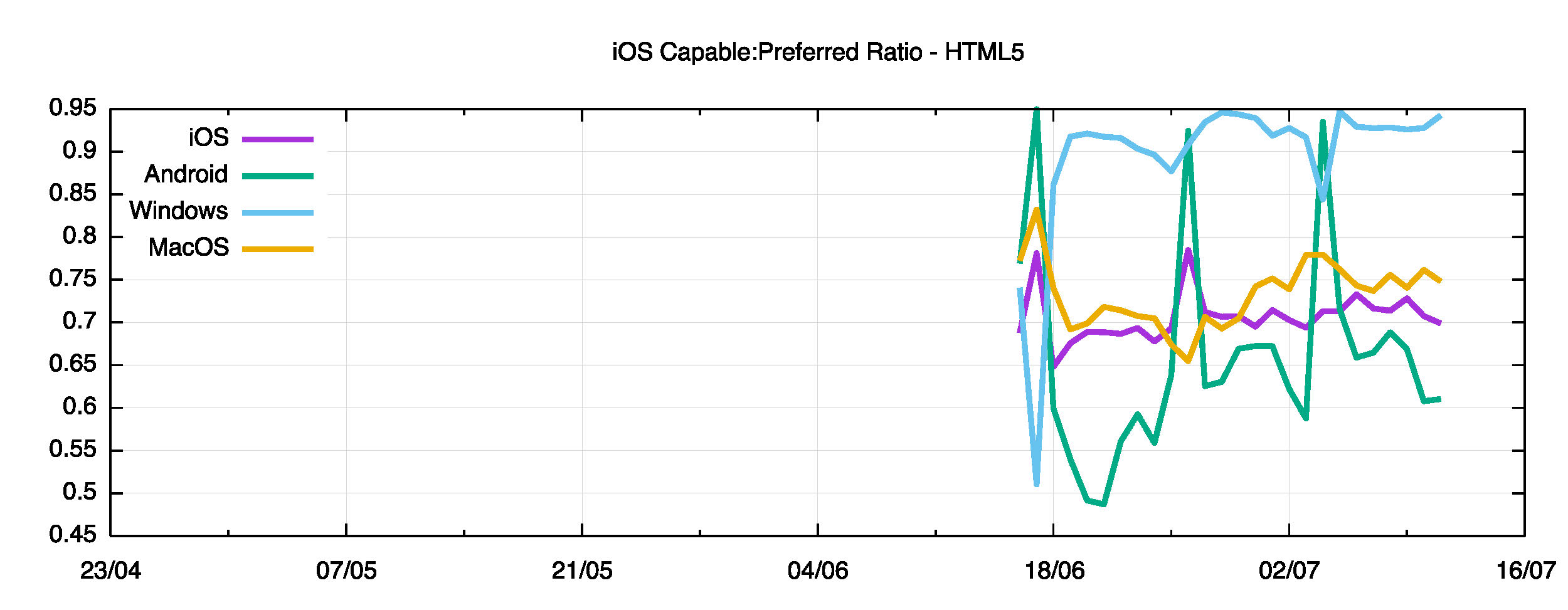
Figure 15 – Capable : Preferred ratio for HTML5
There are three distinct “bands†in Figure 15. Between 90% and 95% of Windows platforms prefer to use IPv6 when they have access to IPv6. The Apple iOS and MacOS platforms have a ratio of 70% – 75%, so that three quarters of Apple platforms will prefer to use IPv6 in those situations where they have IPv6 available. Android devices show a somewhat lower preference ratio, between 60% to 70% of IPv6 Capable Android platforms Preferring to use IPv6.
What Changed?
We now have enough evidence to explain the changes in Figure 2 when we added HTML5 to the advertisement stream. The percentage of IPv6 Capable systems was largely unaltered, showing the same overall growth trend since the start of May. However there is a larger “gap†between capable and preferred, and the preferred number has been steady at between 3.5% to 4% for the past month.
It is evident that the proportion of Windows units has dropped in relative numbers, and instead of making up 95% of all measured platforms, Windows is now approximately some 70% of seen systems. What we are now seeing more of as a result of using HTML5 are mobile devices and mobile networks, and in particular more devices running Apple’s iOS and Google’s Android operating systems. These systems do not strongly prefer IPv6 when given the choice. They use a more nuanced form of relative delay estimation and elect to use IPv6 in preference to IPv4 for dual stack access between 60% to 75% of the time. Therefore, as these systems now make up some 25% of the total mix, their reduced level of preference for IPv6 shows up as an overall reduction in the IPv6 Preference level for the global numbers.
It is clear when looking at IPv6 mobile networks, such as the US mobile network shown in Figure 16, that the advertisement based measurement system is now capable of seeing more clearly into mobile networks and devices.
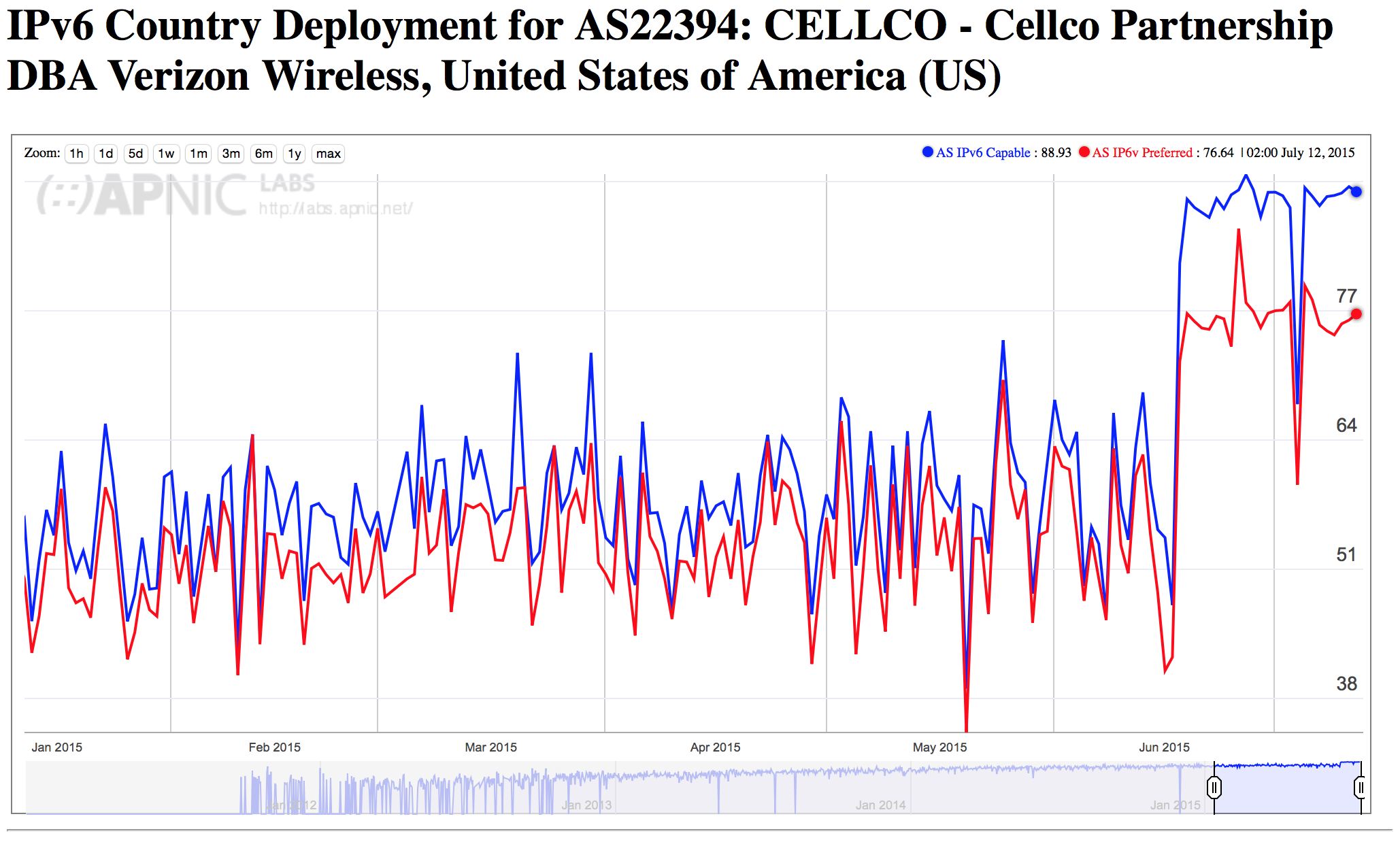
Figure 16 – IPv6 measurements for AS22394
Acknowledgement
We are indebted to Google and Comcast for their generous support of this IPv6 research program, through their support of the advertisement campaigns and the server infrastructure that collects and processes the measurement results.